设 $A$ 是半径为 $5$ 的 $\odot O$ 上的一个定点，单位向量 $\overrightarrow{b}$ 在 $A$ 点处与 $\odot O$ 相切，点 $P$ 是 $\odot O$ 上的一个动点，且点 $P$ 与点 $A$ 不重合，则 $\overrightarrow{AP}\cdot\overrightarrow{b}$ 的取值范围是 ．
【难度】
【出处】
2012年第二十三届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$[-5,5]$
【解析】
如图，根据向量数量积的定义，有$$\overrightarrow{AP}\cdot\overrightarrow{b}=|AP'|\cdot\left|\overrightarrow{b}\right|=|AP'|,$$其中点 $P'$ 是点 $P$ 在 $\overrightarrow{b}$ 上的投影点．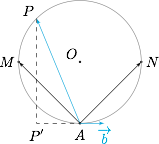
因此当点 $P$ 为点 $M$ 时，取最小值 $-5$；点 $P$ 为点 $N $ 是，取最大值 $ 5 $，结合连续性，$ \overrightarrow{AP}\cdot\overrightarrow{b} $ 的取值范围是 $ [-5,5]$．
因此当点 $P$ 为点 $M$ 时，取最小值 $-5$；点 $P$ 为点 $N $ 是，取最大值 $ 5 $，结合连续性，$ \overrightarrow{AP}\cdot\overrightarrow{b} $ 的取值范围是 $ [-5,5]$．
题目
答案
解析
备注
