已知 $f(x)=\begin{cases}\mathrm{e}^{|\ln x|},&0<x\leqslant 5,\\-x+10,&x>5.\end{cases}$ 若方程 $f(x)=k$ 有三个不同的实数根 $a,b,c$,且 $a<b<c$,则 $ab=$ ,$c$ 的取值范围是 .
【难度】
【出处】
2012年第二十三届“希望杯”全国数学邀请赛高二(一试)
【标注】
【答案】
$1$,$(5,9)$
【解析】
由题函数 $f(x)$ 即$$f(x)=\begin{cases}\dfrac1x,&0<x\leqslant1,\\ x,&1<x\leqslant5,\\-x+10,&x>5.\end{cases}$$如图,题意即$$(a,b,c)=\left(\dfrac1k,k,-k+10\right)$$其中 $k\in(1,5)$,因此 $ab=1$,实数 $c$ 的取值范围为 $(5,9)$.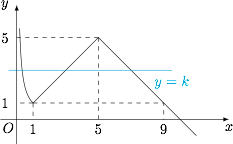
题目
答案
解析
备注