如图,在极坐标系中,过点 $ M\left(2,0\right) $ 的直线 $ l $ 与极轴的夹角 $ \alpha ={\dfrac{{\mathrm \pi } }{6}} $.若将 $ l $ 的极坐标方程写成 $ \rho =f\left(\theta \right) $ 的形式,则 $ f\left(\theta \right)= $ .

【难度】
【出处】
2012年高考上海卷(理)
【标注】
【答案】
$\dfrac{1}{{\sin \left( {\dfrac{\mathrm \pi }{6} - \theta } \right)}}$
【解析】
如图,设 $P\left(\rho,\theta\right) $ 是直线 $ l$ 上任意一点,
在 $ \triangle OPM$ 中,由正弦定理,得 $\dfrac{{\left| {OM} \right|}}{{\sin \left( {\dfrac{\mathrm \pi }{6} - \theta } \right)}} = \dfrac{\rho }{{\sin \dfrac{5\mathrm \pi }{6}}},$
化简,得 $\rho = \dfrac{1}{{\sin \left( {\dfrac{\mathrm \pi }{6} - \theta } \right)}}.$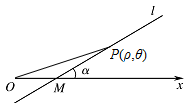
在 $ \triangle OPM$ 中,由正弦定理,得 $\dfrac{{\left| {OM} \right|}}{{\sin \left( {\dfrac{\mathrm \pi }{6} - \theta } \right)}} = \dfrac{\rho }{{\sin \dfrac{5\mathrm \pi }{6}}},$
化简,得 $\rho = \dfrac{1}{{\sin \left( {\dfrac{\mathrm \pi }{6} - \theta } \right)}}.$

题目
答案
解析
备注