在平行四边形 $ ABCD $ 中,$ \angle A={\dfrac{{\mathrm{\pi}} }{3}} $,边 $ AB$,$AD $ 的长分别为 $ 2$,$1 $.若 $ M$,$N $ 分别是边 $ BC$,$CD $ 上的点,且满足 $ \dfrac {\left|{\overrightarrow {BM}}\right|} {\left|{\overrightarrow {BC}}\right|} = \dfrac {\left|{\overrightarrow {CN}}\right|}{\left|{\overrightarrow {CD}}\right|} $,则 $ {\overrightarrow {AM}}\cdot {\overrightarrow {AN}} $ 的取值范围是 .
【难度】
【出处】
2012年高考上海卷(理)
【标注】
【答案】
$ \left[2,5\right] $
【解析】
建立如图所示的直角坐标系,则 $ B(2,0) $,$ A(0,0) $,$D(\dfrac 12,\dfrac {\sqrt3}{2}) $.
设 $ \dfrac {\left|{\overrightarrow {BM}}\right|} {\left|{\overrightarrow {BC}}\right|} = \dfrac {\left|{\overrightarrow {CN}}\right|}{\left|{\overrightarrow {CD}}\right|} =\lambda$,$\lambda \in [0,1] $.
则 $M(2+\dfrac {\lambda}{2},\dfrac {\sqrt 3 \lambda}{2}) $,$ N(\dfrac 52-2\lambda,\dfrac {\sqrt 3}{2})$.
故 $ {\overrightarrow {AM}}\cdot {\overrightarrow {AN}}=-\lambda ^2-2\lambda+5 \in [2,5] $.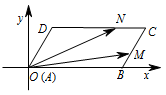
设 $ \dfrac {\left|{\overrightarrow {BM}}\right|} {\left|{\overrightarrow {BC}}\right|} = \dfrac {\left|{\overrightarrow {CN}}\right|}{\left|{\overrightarrow {CD}}\right|} =\lambda$,$\lambda \in [0,1] $.
则 $M(2+\dfrac {\lambda}{2},\dfrac {\sqrt 3 \lambda}{2}) $,$ N(\dfrac 52-2\lambda,\dfrac {\sqrt 3}{2})$.
故 $ {\overrightarrow {AM}}\cdot {\overrightarrow {AN}}=-\lambda ^2-2\lambda+5 \in [2,5] $.

题目
答案
解析
备注