在矩形 $ ABCD $ 中，边 $ AB$，$AD $ 的长分别为 $ 2$，$1 $．若 $ M$，$N $ 分别是边 $ BC$，$CD $ 上的点，且满足 $ \dfrac {\left|{\overrightarrow {BM}} \right| }{\left |{\overrightarrow {BC}} \right|} = \dfrac{ \left|{\overrightarrow {CN}} \right| }{\left|{\overrightarrow {CD}} \right| } $，则 $ {\overrightarrow {AM}}\cdot {\overrightarrow {AN}} $ 的取值范围是 ．
【难度】
【出处】
2012年高考上海卷（文）
【标注】
【答案】
$ [1,4] $
【解析】
如图，以 $A$ 为坐标原点，$AB$，$AD$ 为 $x$，$y$ 轴建立平面直角坐标系．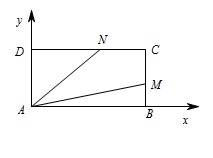
由题可设 $M\left(2,t\right)$，则根据 $ \dfrac {\left|{\overrightarrow {BM}} \right| }{\left |{\overrightarrow {BC}} \right|} = \dfrac{ \left|{\overrightarrow {CN}} \right| }{\left|{\overrightarrow {CD}} \right| } $，可知 $N\left(2-2t,1\right)$，且 $t \in\left[0,1\right]$，即可表达出 $ {\overrightarrow {AM}}\cdot {\overrightarrow {AN}}=4-3t $．
由题可设 $M\left(2,t\right)$，则根据 $ \dfrac {\left|{\overrightarrow {BM}} \right| }{\left |{\overrightarrow {BC}} \right|} = \dfrac{ \left|{\overrightarrow {CN}} \right| }{\left|{\overrightarrow {CD}} \right| } $，可知 $N\left(2-2t,1\right)$，且 $t \in\left[0,1\right]$，即可表达出 $ {\overrightarrow {AM}}\cdot {\overrightarrow {AN}}=4-3t $．
题目
答案
解析
备注
