已知函数 $f(x)=\begin{cases} \big|\log_3x\big|,&0<x\leqslant 3,\\-x+4,&x>3,\end{cases}$ 若 $a<b<c$，且 $f(a)=f(b)=f(c)$，则 $(ab+2)^c$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$(27,81)$
【解析】
函数 $f(x)$ 的图象如下．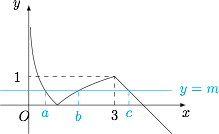
设 $f(a)=f(b)=f(c)=m$，则\[\begin{split} -{\log_3}a=m,\\ {\log_3}b=m,\\ -c+4=m,\end{split}\]因此\[(ab+2)^c=\left(3^{-m}\cdot 3^m+2\right)^{4-m}=3^{4-m},\]其中 $0<m<1$．因此所求代数式的取值范围是 $(27,81)$．
设 $f(a)=f(b)=f(c)=m$，则\[\begin{split} -{\log_3}a=m,\\ {\log_3}b=m,\\ -c+4=m,\end{split}\]因此\[(ab+2)^c=\left(3^{-m}\cdot 3^m+2\right)^{4-m}=3^{4-m},\]其中 $0<m<1$．因此所求代数式的取值范围是 $(27,81)$．
题目
答案
解析
备注
