已知抛物线 $y=ax^2+bx$ 过点 $A(4,0)$,若点 $B(x,y)$ 为该抛物线在第一象限内的一个动点,且使得 $\triangle{AOB}$ 的面积取到最大值 $8$,则 $a+b=$ .
【难度】
【出处】
2015年第二十六届“希望杯”全国数学邀请赛高一(二试)
【标注】
【答案】
$3$
【解析】
根据题意,抛物线 $y=ax^2+bx$ 的两个零点为 $x=0$ 和 $x=4$,所以$$y=ax(x-4).$$因为 $\triangle AOB$ 面积的最大值为 $8$,所以 $B$ 点的纵坐标的最大值为 $4$,所以抛物线开口向下,且 $B$ 为抛物线的顶点,得到抛物线的方程为 $y=-x(x-4)$,于是 $a+b=-1+4=3$.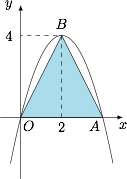

题目
答案
解析
备注