已知平面直角坐标系中，点 $B(2,0)$，点 $A$ 在线段 $OB$ 上，$AB=\sqrt 2$，将线段 $OB$ 绕点 $O$ 按逆时针方向旋转角 $\alpha$（$0<\alpha<\pi$）到点 $B'$，点 $A$ 到点 $A'$，对于 $y$ 轴上的点 $P$，若 $\triangle{B'PA'}$ 是以 $\angle{B'}$ 为顶角的等腰三角形，则 $\alpha$ 的取值范围是 ．
【难度】
【出处】
2015年第二十六届“希望杯”全国数学邀请赛高一（二试）
【标注】
【答案】
$\left[\dfrac {\pi}{4},\dfrac{\pi}{2}\right)\cup\left(\dfrac{\pi}{2},\dfrac{3}{4}\pi\right]$
【解析】
如图．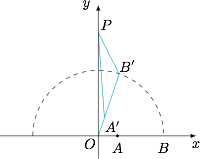
旋转后 $B'(2\cos \alpha,2\sin \alpha)$，若存在 $\triangle{B'PA'}$ 是以 $B'$ 为顶角的等腰三角形，则$$|2\cos \alpha|\leqslant \sqrt 2,$$且 $A',B',P$ 不共线，解得 $\alpha$ 的取值范围是 $\left[\dfrac {\pi}{4},\dfrac{\pi}{2}\right)\cup\left(\dfrac{\pi}{2},\dfrac{3}{4}\pi\right]$．
旋转后 $B'(2\cos \alpha,2\sin \alpha)$，若存在 $\triangle{B'PA'}$ 是以 $B'$ 为顶角的等腰三角形，则$$|2\cos \alpha|\leqslant \sqrt 2,$$且 $A',B',P$ 不共线，解得 $\alpha$ 的取值范围是 $\left[\dfrac {\pi}{4},\dfrac{\pi}{2}\right)\cup\left(\dfrac{\pi}{2},\dfrac{3}{4}\pi\right]$．
题目
答案
解析
备注
