已知函数 $ y={\dfrac{|x^2-1|}{x-1}} $ 的图象与函数 $ y=kx $ 的图象恰有两个交点，则实数 $ k $ 的取值范围是 ．
【难度】
【出处】
2012年高考天津卷（文）
【标注】
【答案】
$ \left(0,1\right) \cup\left( 1,2\right) $
【解析】
根据已知，得 $f\left(x\right)= \begin{cases}x+1,&x\leqslant -1或x>1,\\-x-1,&-1<x<1.\end{cases}$
如图，当 $k$ 值不断变化时，交点个数随之发生变化；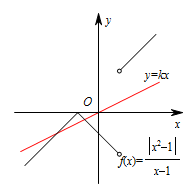
因此，恰有两个交点时，实数 $k$ 的取值范围是 $\left(0,1\right)\cup\left(1,2\right)$．
如图，当 $k$ 值不断变化时，交点个数随之发生变化；
因此，恰有两个交点时，实数 $k$ 的取值范围是 $\left(0,1\right)\cup\left(1,2\right)$．
题目
答案
解析
备注
