已知四面体 $ABCD$，$AB=AC=AD=BC=BD=1$，$CD=\sqrt2$，则该四面体的内切球半径等于 ．
【难度】
【出处】
2011年第二十二届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$\sqrt2-\dfrac{\sqrt6}{2}$
【解析】
取 $CD$ 中点，记为 $E$，连接 $AE,BE$，如图．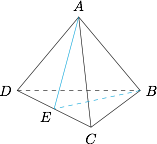
由题可知 $AE\perp CD,BE\perp CD$，则$$V_{A-BCD}=\dfrac13\cdot S_{\triangle ABE}\cdot CD=\dfrac{\sqrt3}{12},$$设内切球半径为 $r$，四面体 $ABCD$ 的表面积为 $S$，则有$$r=\dfrac{3V}{S}=\sqrt2-\dfrac{\sqrt6}{2}.$$
由题可知 $AE\perp CD,BE\perp CD$，则$$V_{A-BCD}=\dfrac13\cdot S_{\triangle ABE}\cdot CD=\dfrac{\sqrt3}{12},$$设内切球半径为 $r$，四面体 $ABCD$ 的表面积为 $S$，则有$$r=\dfrac{3V}{S}=\sqrt2-\dfrac{\sqrt6}{2}.$$
题目
答案
解析
备注
