已知边长为 $2$ 的等边 $\triangle ABC$ 的顶点 $A$ 和 $B$ 分别在 $y=\sqrt3x$（$y\geqslant0$）和 $y=0$（$x\leqslant0$）上移动，并且顶点 $A,B,C$ 按顺时针方向放置，则顶点 $C$ 的轨迹方程是 ．
【难度】
【出处】
2011年第二十二届“希望杯”全国数学邀请赛高二（二试）
【标注】
【答案】
$y=-\sqrt3x,-\dfrac{2\sqrt3}{3}\leqslant x\leqslant 1$
【解析】
如图，连接 $OC$．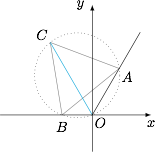
由题可知$$\angle AOB=120^\circ,\angle C=60^\circ,$$因此 $O,A,C,B$ 四点共圆，故$$\angle AOC=\angle BOC=60^\circ,$$因此点 $C(x,y)$ 恒在直线 $y=-\sqrt3x$ 上，注意到点 $O$ 在弧 $AB$ 上，因此$$2\leqslant OC\leqslant \dfrac{4}{\sqrt3},$$故点 $C$ 的横坐标$$1\leqslant x\leqslant\dfrac{2\sqrt3}{3},$$因此顶点 $C$ 的轨迹方程是 $y=-\sqrt3x,-\dfrac{2\sqrt3}{3}\leqslant x\leqslant 1$．
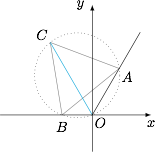由题可知$$\angle AOB=120^\circ,\angle C=60^\circ,$$因此 $O,A,C,B$ 四点共圆，故$$\angle AOC=\angle BOC=60^\circ,$$因此点 $C(x,y)$ 恒在直线 $y=-\sqrt3x$ 上，注意到点 $O$ 在弧 $AB$ 上，因此$$2\leqslant OC\leqslant \dfrac{4}{\sqrt3},$$故点 $C$ 的横坐标$$1\leqslant x\leqslant\dfrac{2\sqrt3}{3},$$因此顶点 $C$ 的轨迹方程是 $y=-\sqrt3x,-\dfrac{2\sqrt3}{3}\leqslant x\leqslant 1$．
题目
答案
解析
备注
