已知 $f\left( x \right) = m\left( {x - 2m} \right)\left( {x + m + 3} \right)$，$g\left( x \right) = {2^x} - 2$．若同时满足条件：
① $\forall x \in {\mathbb{R}}$，$f\left( x \right) < 0$ 或 $g\left( x \right) < 0$；
② $\exists x \in \left( { - \infty , - 4} \right),f\left( x \right)g\left( x \right) < 0$，
则 $m$ 的取值范围是 ．
① $\forall x \in {\mathbb{R}}$，$f\left( x \right) < 0$ 或 $g\left( x \right) < 0$；
② $\exists x \in \left( { - \infty , - 4} \right),f\left( x \right)g\left( x \right) < 0$，
则 $m$ 的取值范围是
【难度】
【出处】
2012年高考北京卷（理）
【标注】
【答案】
$ \left(-4,-2\right) $
【解析】
本题对二次函数和指数函数的图象和性质进行了综合的考查，结合函数的图象，对 $m$ 进行分类讨论即可．满足题意的大致图象如下：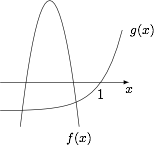
对于 ①，当 $ x<1 $ 时，$ g\left(x\right)<0 $．因为 $\forall x \in {\mathbb R}$，$ f\left(x\right)<0 $ 或 $ g\left(x\right)<0 $，
所以 $f\left(x\right)=m\left(x-2m\right)\left(x+m+3\right)<0 $ 在 $ x\geqslant 1 $ 时恒成立．
由二次函数的性质，可知抛物线开口向下，且与 $ x $ 轴的交点都在 $\left(1,0\right)$ 的左侧，
于是\begin{align*}
m&<0,\\
-m-3&<1,\\
2m&<1,
\end{align*}解得 $ -4<m<0$．
又因为 $\exists x \in \left( { - \infty , - 4} \right)$，$f\left( x \right)g\left( x \right) < 0$，而此时 $g\left( x \right) = {2^x} - 2 < 0$ 恒成立，
所以\[
\exists x \in \left( { - \infty , - 4} \right), f(x)>0,
\]从而只要 $ -4 $ 大于 $ 2m,-m-3$ 中较小的数即可．
（1）当 $ - 1 < m < 0$ 时，$ -m-3<2m$，但是 $-m-3>-4$，不成立；
（2）当 $ m=-1 $ 时，$2m=-m-3=-2>-4$，不成立；
（3）当 $ -4<m<-1 $ 时，$2m<-m-3$，此时进一步要求 $ 2m<-4 $，即 $-4<m<-2$，成立．
综上所述，当 ①② 同时成立时，有 $ -4<m<-2 $．
对于 ①，当 $ x<1 $ 时，$ g\left(x\right)<0 $．因为 $\forall x \in {\mathbb R}$，$ f\left(x\right)<0 $ 或 $ g\left(x\right)<0 $，所以 $f\left(x\right)=m\left(x-2m\right)\left(x+m+3\right)<0 $ 在 $ x\geqslant 1 $ 时恒成立．
由二次函数的性质，可知抛物线开口向下，且与 $ x $ 轴的交点都在 $\left(1,0\right)$ 的左侧，
于是\begin{align*}
m&<0,\\
-m-3&<1,\\
2m&<1,
\end{align*}解得 $ -4<m<0$．
又因为 $\exists x \in \left( { - \infty , - 4} \right)$，$f\left( x \right)g\left( x \right) < 0$，而此时 $g\left( x \right) = {2^x} - 2 < 0$ 恒成立，
所以\[
\exists x \in \left( { - \infty , - 4} \right), f(x)>0,
\]从而只要 $ -4 $ 大于 $ 2m,-m-3$ 中较小的数即可．
（1）当 $ - 1 < m < 0$ 时，$ -m-3<2m$，但是 $-m-3>-4$，不成立；
（2）当 $ m=-1 $ 时，$2m=-m-3=-2>-4$，不成立；
（3）当 $ -4<m<-1 $ 时，$2m<-m-3$，此时进一步要求 $ 2m<-4 $，即 $-4<m<-2$，成立．
综上所述，当 ①② 同时成立时，有 $ -4<m<-2 $．
题目
答案
解析
备注
