查看数据源：59f4aefdae6f3a0008e3e6cd
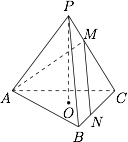
正三棱锥 $P-ABC$ 中，$2PM=CM$，$CN=2NB$，有下列命题：
① 二面角 $B-PA-C$ 的大小的取值范围是 $\left(\dfrac{\pi}3,\pi\right)$；
② 若 $MN\perp AM$，则 $PC$ 与面 $PAB$ 所成角的大小为 $\dfrac{\pi}2$；
③ 过点 $M$ 与异面直线 $PA$ 与 $BC$ 都成 $\dfrac{\pi}4$ 的直线有 $3$ 条；
④ 若二面角 $B-PA-C$ 大小为 $\dfrac{2\pi}3$，则过点 $N$ 与平面 $PAC$ 与平面 $PAB$ 都成 $\dfrac{\pi}6$ 的直线有 $3$ 条．其中所有正确的命题的序号是 ．
【难度】
【出处】
无
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何量
    >
    空间的角
【答案】
①②④
【解析】
命题 ①  设底面中心为 $O$，当 $P$ 从 $O$ 运动到无穷远（此时三棱锥近似成为三棱柱），二面角 $B-PA-C$ 的大小的取值范围为 $\left(\dfrac{\pi}3,\pi\right)$，命题正确．命题 ② 根据题意，有\[\left.\begin{split}\left.\begin{split}\dfrac{PM}{CM}=\dfrac{BN}{CN}\Rightarrow MN\parallel PB, \\ AM\perp MN,\end{split}\right\}\Rightarrow PB\perp AM,\\ PB\perp AC\end{split}\right\}\Rightarrow PB\perp AMC\Rightarrow PB\perp PC,\\ PC\perp AB\]进而可得 $PA,PB,PC$ 两两垂直，命题正确．
命题 ③ 由于 $PA$ 与 $BC$ 所成的角为 $\dfrac{\pi}2$，因此符合条件的直线有 $2$ 条，命题错误．
命题 ④ 平面 $PAC$ 与平面 $PAB$ 的法线所成的角为 $\dfrac{\pi}3$，因此过点 $N$ 与这两条法线所成角都为 $\dfrac{\pi}3$ 的直线有 $3$ 条，命题正确．
综上所述，命题 ①②④ 正确．
题目 答案 解析 备注
0.112281s