已知三棱锥 $S - ABC$ 的底面 $ABC$ 为正三角形，点 $A$ 在侧面 $SBC$ 上的射影 $H$ 是 $\triangle SBC$ 的垂心，二面角 $H - AB - C$ 为 $30^\circ $，且 $SA = 2$，则此三棱锥的体积为 \((\qquad)\)
【难度】
【出处】
2012年清华大学（高水平大学）自主选拔学业能力测试
【标注】
【答案】
D
【解析】
如图，设 $S$ 在底面上的投影为 $O$，延长 $SH,BH$ 分别交 $BC,SC$ 于 $P,Q$ 两点，如图：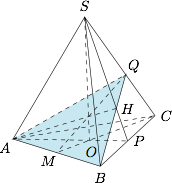
因为 $AH \perp SBC$，则 $ABQ \perp SBC$；
由题意 $H$ 为 $\triangle SBC$ 的垂心，则 $SC \perp BQ$，且 $ABQ\cap SBC=BQ$，故 $SC \perp ABQ$，因此 $SC\perp AB$，所以 $OC \perp AB$，同理有 $AO\perp BC$，因此 $O$ 为 $\triangle ABC$ 的垂心，即中心．也即 $S - ABC$ 为正三棱锥．
取 $AB$ 的中点 $M$，则 $\angle QMC$ 为二面角 $H - AB - C$ 的平面角，$\angle QMC = 30^\circ $，$\angle QCM = 60^\circ $．
于是 $OC = SC\cdot\cos \angle QCM = 2 \cdot \cos 60^\circ = 1$，底面 $\triangle ABC$ 边长为 $\sqrt 3 $．
因此三棱锥体积为 $\dfrac{3}{4}$．
因为 $AH \perp SBC$，则 $ABQ \perp SBC$；由题意 $H$ 为 $\triangle SBC$ 的垂心，则 $SC \perp BQ$，且 $ABQ\cap SBC=BQ$，故 $SC \perp ABQ$，因此 $SC\perp AB$，所以 $OC \perp AB$，同理有 $AO\perp BC$，因此 $O$ 为 $\triangle ABC$ 的垂心，即中心．也即 $S - ABC$ 为正三棱锥．
取 $AB$ 的中点 $M$，则 $\angle QMC$ 为二面角 $H - AB - C$ 的平面角，$\angle QMC = 30^\circ $，$\angle QCM = 60^\circ $．
于是 $OC = SC\cdot\cos \angle QCM = 2 \cdot \cos 60^\circ = 1$，底面 $\triangle ABC$ 边长为 $\sqrt 3 $．
因此三棱锥体积为 $\dfrac{3}{4}$．
题目
答案
解析
备注
