在正方体 $ABCD-A_1B_1C_1D_1$ 中，直线 $BD_1$ 与平面 $ABCD$ 所成角的正切值是 ．
【难度】
【出处】
2010年第二十一届“希望杯”全国数学邀请赛高一（一试）
【标注】
【答案】
$\dfrac{\sqrt 2}{2}$
【解析】
如图．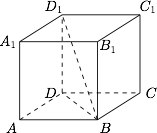
如图，$\angle{DBD_1}$ 即为直线 $BD_1$ 与平面 $ABCD$ 所成角，易知\[\tan {\angle{DBD_1}}=\dfrac{DD_1}{BD}=\dfrac{\sqrt 2}{2}.\]
如图，$\angle{DBD_1}$ 即为直线 $BD_1$ 与平面 $ABCD$ 所成角，易知\[\tan {\angle{DBD_1}}=\dfrac{DD_1}{BD}=\dfrac{\sqrt 2}{2}.\]
题目
答案
解析
备注
