已知直线 $y=kx-2$（$k>0$）与抛物线 $y=\dfrac18x^2$ 相交于 $A,B$ 两点，$F$ 是抛物线的焦点，$|FA|=2|FB|$，则 $k=$ ．
【难度】
【出处】
2010年第二十一届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$\dfrac{3\sqrt2}{4}$
【解析】
连接 $AF,BF,BO$，过点 $A,B$ 分别作准线 $y=-2$ 的垂线，垂足分别为 $M,N$，如图．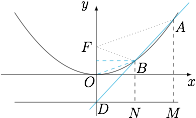
根据抛物线的定义，可得$$AM=2BN,AM\parallel BN,$$因此点 $B$ 是 $AD$ 中点，进而在 $\triangle DAF$ 中，$$OB=\dfrac12AF,$$所以 $\triangle BOF$ 是以点 $B$ 为顶点的等腰三角形，则点 $B$ 纵坐标为 $1$，因此$$B\left(2\sqrt2,1\right),$$因此计算得 $k$ 的值为 $\dfrac{3\sqrt2}{4}$．
根据抛物线的定义，可得$$AM=2BN,AM\parallel BN,$$因此点 $B$ 是 $AD$ 中点，进而在 $\triangle DAF$ 中，$$OB=\dfrac12AF,$$所以 $\triangle BOF$ 是以点 $B$ 为顶点的等腰三角形，则点 $B$ 纵坐标为 $1$，因此$$B\left(2\sqrt2,1\right),$$因此计算得 $k$ 的值为 $\dfrac{3\sqrt2}{4}$．
题目
答案
解析
备注
