已知点 $P(x,y)$ 在曲线 $x^2+y^2-|x|-|y|=0$ 上，设 $O$ 为坐标原点，则 $|OP|$ 的最小值是 ，最大值是 ．
【难度】
【出处】
2010年第二十一届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$0$；$\sqrt2$
【解析】
由题可知曲线 $x^2+y^2-|x|-|y|=0$ 关于坐标轴对称，在每个象限内图象均为半圆，如图．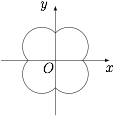
当点 $P$ 为原点 $O$ 时，$|OP|$ 最小为 $0$，当 $|OP|$ 为圆的直径时，取得最大值 $\sqrt2$．
当点 $P$ 为原点 $O$ 时，$|OP|$ 最小为 $0$，当 $|OP|$ 为圆的直径时，取得最大值 $\sqrt2$．
题目
答案
解析
备注
