查看数据源：5910286140fdc7000841c6e4
将一个正 $11$ 边形用对角线划分为 $9$ 个三角形，这些对角线在正 $11$ 边形内两两不相交，则 \((\qquad)\)
A: 存在某种分法，所分出的三角形都不是锐角三角形
B: 存在某种分法，所分出的三角形恰有两个锐角三角形
C: 存在某种分法，所分出的三角形至少有 $3$ 个锐角三角形
D: 任何一种分法所分出的三角形都恰有 $1$ 个锐角三角形
【难度】
【出处】
2011年清华大学等七校联考自主招生试题
【标注】
  • 数学竞赛
    >
    简单组合
    >
    简单组合
  • 题型
    >
    组合数学
    >
    组合证明
【答案】
D
【解析】
我们先证明分出的三角形中至多只有一个锐角三角形．如图，假设 $\triangle ABC$ 是锐角三角形，我们证明另一个三角形 $\triangle DEF$（不妨设在 $AC$ 的另一边）的（其中的边 $EF$ 有可能与 $AC$ 重合）的 $\angle D$ 一定是钝角．事实上，$\angle D\geqslant\angle ADC$，而四边形 $ABCD$ 是圆内接四边形，所以 $\angle ADC=180^\circ-\angle B$，所以 $\angle D$ 为钝角．这样就排除了B，C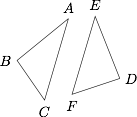．下面证明所分出的三角形中至少有一个锐角三角形．
因为中心不在任何一条对角线上，所以中心必包含在某个三角形中，这个三角形一定是锐角三角形，所以答案是D．
题目 答案 解析 备注
0.110747s