查看数据源：59fa749c6ee16400083d26c7
正棱柱 $ABCD-A_1B_1C_1D_1$ 中，$AB=1,AA_1=2$，点 $P$ 在 $BD_1$ 上，过点 $P$ 作平面 $BB_1D_1D$ 的垂线，与题设的正四棱柱的表面相交于 $M,N$ 两点，记 $BP=x,MN=y$，则 $x$ 与 $y$ 之间的函数式是 $y=f(x)=$  ，此函数的值域是 ．
【难度】
【出处】
2010年第二十一届“希望杯”全国数学邀请赛高二（一试）
【标注】
  • 方法
    >
    思考方式
    >
    数学建模
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的截面
【答案】
$\begin{cases}\dfrac{2\sqrt3}{3}x,&0<x\leqslant\dfrac{\sqrt6}{2}\\-\dfrac{2\sqrt3}{3}x+3\sqrt2,&\dfrac{\sqrt6}{2}<x<\sqrt6\end{cases}$；$\left(0,\sqrt2\right]$
【解析】
取 $AA_1,CC_1$ 中点，分别记为 $E,F$，连接 $EF$ 交 $BD_1$ 于点 $Q$，则 $Q$ 为 $BD_1$ 中点，如图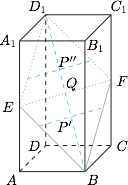．由题可知过点 $P$ 且垂直于面 $BB_1D_1D$ 的直线在平面 $EBFD_1$ 上．
当 $P$ 点在线段 $BQ$ 上时，由 $\triangle BMN$ 与 $\triangle BEF$ 相似，得$$\dfrac{x}{y}=\dfrac{\dfrac{\sqrt6}{2}}{\sqrt2},$$当 $P$ 点在线段 $QD_1$ 上时，由 $\triangle D_1EF$ 与 $\triangle DMN$ 相似，得$$\dfrac{\sqrt6-\left(x-\dfrac{\sqrt6}{2}\right)}{y}=\dfrac{\dfrac{\sqrt6}{2}}{\sqrt2},$$因此 $x,y$ 之间的函数表达式为$$y=f(x)=\begin{cases}\dfrac{2\sqrt3}{3}x,&0<x\leqslant\dfrac{\sqrt6}{2}\\-\dfrac{2\sqrt3}{3}x+3\sqrt2,&\dfrac{\sqrt6}{2}<x<\sqrt6\end{cases}$$此函数的值域是 $\left(0,\sqrt2\right]$．
题目 答案 解析 备注
0.109862s