过双曲线 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ 的右焦点的直线交双曲线的右支于 $A,B$ 两点，设 $F$ 是双曲线的左焦点，$e$ 是双曲线的离心率，若 $\triangle ABF$ 是等腰三角形．且 $\angle A=90^\circ$，则 $e^2=$ ．
【难度】
【出处】
2010年第二十一届“希望杯”全国数学邀请赛高二（二试）
【标注】
【答案】
$5-2\sqrt2$
【解析】
设双曲线的右焦点为 $F_1$，如图．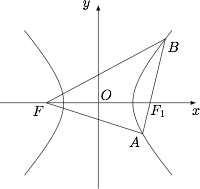
设 $AF_1=x$，则$$AF=2a+x,BF_1=2a,BF=4a,$$再结合 $\triangle ABF$ 为等腰直角三角形，则$$BF=\sqrt2AF=\sqrt2(2a+x)=4a,$$解得 $x=\left(2\sqrt2-2\right)a$，再结合 $\triangle AFF_1$ 是直角三角形，有$$(2c)^2=\left(2\sqrt2a\right)^2+\left[\left(2\sqrt2-2\right)a\right]^2,$$解得 $e^2=5-2\sqrt2$．
设 $AF_1=x$，则$$AF=2a+x,BF_1=2a,BF=4a,$$再结合 $\triangle ABF$ 为等腰直角三角形，则$$BF=\sqrt2AF=\sqrt2(2a+x)=4a,$$解得 $x=\left(2\sqrt2-2\right)a$，再结合 $\triangle AFF_1$ 是直角三角形，有$$(2c)^2=\left(2\sqrt2a\right)^2+\left[\left(2\sqrt2-2\right)a\right]^2,$$解得 $e^2=5-2\sqrt2$．
题目
答案
解析
备注
