已知直角梯形 $ABCD$ 中，$AD\parallel BC$，$\angle ADC = 90^\circ $，$AD = 2$，$BC = 1$，$P$ 是腰 $DC$ 上的动点，则 $\left| {\overrightarrow {PA} + 3\overrightarrow {PB} } \right|$ 的最小值为 ．
【难度】
【出处】
2011年高考天津卷（理）
【标注】
【答案】
$5$
【解析】
设 $A(2,0)$，$B(1,m)$，$C(0,m)$，$D(0,0)$，$\overrightarrow{DP}=\lambda \overrightarrow{DC}$（$0\leqslant \lambda \leqslant 1$），则 $P$ 点坐标为 $(0,m\lambda)$．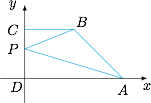
于是有$$ {\overrightarrow {PA} + 3\overrightarrow {PB} }=(5,(3-4\lambda )m),$$于是$$\left| {\overrightarrow {PA} + 3\overrightarrow {PB} } \right|^2=25+(3-4\lambda)^2\cdot m^2 \geqslant 25,$$当 $\lambda =\dfrac 34$ 时 $\left| {\overrightarrow {PA} + 3\overrightarrow {PB} } \right|$ 最小，最小值为 $5$．
于是有$$ {\overrightarrow {PA} + 3\overrightarrow {PB} }=(5,(3-4\lambda )m),$$于是$$\left| {\overrightarrow {PA} + 3\overrightarrow {PB} } \right|^2=25+(3-4\lambda)^2\cdot m^2 \geqslant 25,$$当 $\lambda =\dfrac 34$ 时 $\left| {\overrightarrow {PA} + 3\overrightarrow {PB} } \right|$ 最小，最小值为 $5$．
题目
答案
解析
备注
