将整数 $1,2,3,\cdots ,25$ 填入如图所示的 $5$ 行 $5$ 列的表格中，使每一行的数字从左到右都成递增数列，则第三列各数之和的最小值为 ，最大值为 ．
【难度】
【出处】
无
【标注】
【答案】
$45$；$85$
【解析】
随意填表，然后将每行从左到右递增排列即可得到符合题意的填表方式．
中间一列的数为 $a_1,a_2,a_3,a_4,a_5$，不妨设 $a_1<a_2<a_3<a_4<a_5$，则 $a_i$ 至少比 $3i-1$ 个数大，即 $a_i\geqslant 3i$，于是$$a_1+a_2+a_3+a_4+a_5\geqslant 45,$$如下图，等号可以取到．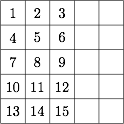
每个符合题意的填表方式可以将所有的数 $x$ 改为 $26-x$，然后关于第三列作对称得到另一种符合题意的填表方式，且为一一对应，因此所求最大值为 $130-45=85$．
中间一列的数为 $a_1,a_2,a_3,a_4,a_5$，不妨设 $a_1<a_2<a_3<a_4<a_5$，则 $a_i$ 至少比 $3i-1$ 个数大，即 $a_i\geqslant 3i$，于是$$a_1+a_2+a_3+a_4+a_5\geqslant 45,$$如下图，等号可以取到．
每个符合题意的填表方式可以将所有的数 $x$ 改为 $26-x$，然后关于第三列作对称得到另一种符合题意的填表方式，且为一一对应，因此所求最大值为 $130-45=85$．
题目
答案
解析
备注
