设 $m > 1$，在约束条件 ${\begin{cases}
y \geqslant x \\
y \leqslant mx \\
x + y \leqslant 1 \\
\end{cases}}$ 下，目标函数 $z = x + 5y$ 的最大值为 $ 4 $，则 $m$ 的值为 ．
y \geqslant x \\
y \leqslant mx \\
x + y \leqslant 1 \\
\end{cases}}$ 下，目标函数 $z = x + 5y$ 的最大值为 $ 4 $，则 $m$ 的值为
【难度】
【出处】
无
【标注】
【答案】
$3$
【解析】
画出可行域，如图，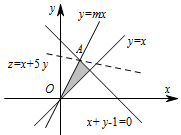
可知 $z = x + 5y$ 在点 $A\left( {\dfrac{1}{1 + m},\dfrac{m}{1 + m}} \right)$ 处取最大值 $ 4$，解得 $m =3 $．
可知 $z = x + 5y$ 在点 $A\left( {\dfrac{1}{1 + m},\dfrac{m}{1 + m}} \right)$ 处取最大值 $ 4$，解得 $m =3 $．
题目
答案
解析
备注
