已知正三棱柱 $ABC-A'B'C'$ 的正（主）视图和侧（左）视图如图所示．设 $\triangle{ABC}$，$\triangle{A'B'C'}$ 的中心分别是 $O$，$O'$，现将此三棱柱绕直线 $OO'$ 旋转，射线 $OA$ 旋转所成的角为 $x$ 弧度（$x$ 可以取到任意一个实数），对应的俯视图的面积为 $S(x)$，则函数 $S(x)$ 的最大值为 ；最小正周期为 ．
说明：“三棱柱绕直线 $OO'$ 旋转”包括逆时针方向和顺时针方向，逆时针方向旋转时，$OA$ 旋转所成的角为正角，顺时针方向旋转时，$OA$ 旋转所成的角为负角．
说明：“三棱柱绕直线 $OO'$ 旋转”包括逆时针方向和顺时针方向，逆时针方向旋转时，$OA$ 旋转所成的角为正角，顺时针方向旋转时，$OA$ 旋转所成的角为负角．【难度】
【出处】
无
【标注】
【答案】
$4\sqrt 3$，$\dfrac{\pi}{3}$
【解析】
这是一个动态几何问题．
依题意，旋转轴 $OO'$ 与俯视图的投影面平行，因此三棱柱的俯视图为长度 $l$ 固定（为 $4$）宽度 $w$ 在变化的矩形，如图所示．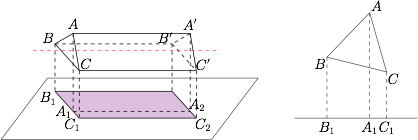
于是$$S(x)=w(x)\cdot l,$$问题转化为研究正三棱柱的底面的投影（为一条线段）长度 $w$ 与旋转角 $x$ 的函数关系．
如图，$w(x)$ 在 $[a\cos {30^{\circ}},a]$ 之间变化，其中 $a$ 为正三棱柱底面边长，分段研究其函数图象．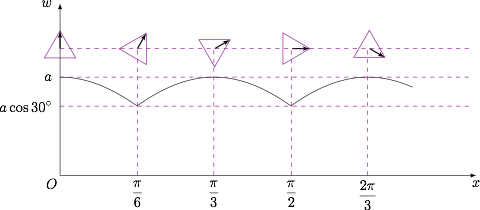
由图象可知 $S(x)$ 的最大值为 $a\cdot l=4\sqrt 3$，最小正周期为 $\dfrac{\pi}{3}$．
依题意，旋转轴 $OO'$ 与俯视图的投影面平行，因此三棱柱的俯视图为长度 $l$ 固定（为 $4$）宽度 $w$ 在变化的矩形，如图所示．
于是$$S(x)=w(x)\cdot l,$$问题转化为研究正三棱柱的底面的投影（为一条线段）长度 $w$ 与旋转角 $x$ 的函数关系．如图，$w(x)$ 在 $[a\cos {30^{\circ}},a]$ 之间变化，其中 $a$ 为正三棱柱底面边长，分段研究其函数图象．
由图象可知 $S(x)$ 的最大值为 $a\cdot l=4\sqrt 3$，最小正周期为 $\dfrac{\pi}{3}$．
题目
答案
解析
备注
