查看数据源：59278f2374a309000798cdd2
在平面直角坐标系中，定义点 $P\left( {{x_1},{y_1}} \right)$、$Q\left( {{x_2},{y_2}} \right)$ 之间的“直角距离”为 $d\left( {P,Q} \right) = \left| {{x_1} - {x_2}} \right| + \left| {{y_1} - {y_2}} \right|$．若 $C\left( {x,y} \right)$ 到点 $A\left( {1,3} \right)$，$B\left( {6,9} \right)$ 的"直角距离"相等，其中实数 $x,y$ 满足 $0 \leqslant x \leqslant 10$，$0 \leqslant y \leqslant 10$，则所有满足条件点 $C$ 的轨迹的长度之和为  ．
【难度】
【出处】
2008年全国高中数学联赛湖南省预赛
【标注】
  • 题型
    >
    立体几何
    >
    立体几何创新题
  • 方法
    >
    思考方式
    >
    信息迁移
【答案】
$5+5\sqrt 2$
【解析】
如图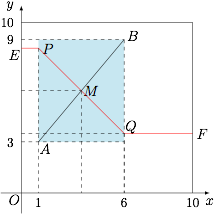．① 显然 $AB$ 的中点 $M$ 满足要求；
② 进而在矩形 $AB$ 内部可以得到斜率为 $-1$ 的线段 $PQ$ 上的点满足要求；
③ 在矩形外部斜率为 $0$ 的线段 $PE$、$QF$ 满足要求．
因此所有满足条件的点 $C$ 的轨迹的长度之和为 $5+5\sqrt 2$．
题目 答案 解析 备注
0.107666s