查看数据源：59278f7174a309000798cdd6
在平面直角坐标系中，定义两点间的“折线距离”及点到曲线的“折线距离”如下：
① $P(x_1,y_1)$，$Q(x_2,y_2)$ 两点之间的“折线距离”$||PQ||$ 为 $|x_1-x_2|+|y_1-y_2|$；
② 若 $P$ 为定点，$Q$ 为曲线 $C$ 的动点，且 $||PQ||$ 存在最小值，则称 $d$ 为点 $P$ 到曲线 $C$ 的“折线距离”．
已知 $O$ 为坐标原点，$A(2,3)$，$F_1(-1,0)$，$F_2(1,0))$．
$(1)$ $||AF_1||=$  ，若点 $M(x,y)$ 满足 $||MA||+||MF_1||=||AF_1||$，则点 $M$ 的轨迹的面积为  ；
$(2)$ 若点 $M(x,y)$ 满足 $||MA||=1$，则点 $M$ 的轨迹所围成的面积为  ；
$(3)$ 若点 $M(x,y)$ 满足 $||MF_1||+||MF_2||=4$，则点 $M$ 的轨迹的周长为  ；
$(4)$ 若点 $M(x,y)$ 满足 $||MF_1||-||MF_2||=1$，则原点 $O$ 到点 $M$ 的轨迹的“折线距离”为  ；
$(5)$ 设直线 $l:x=-1$，若动点 $M(x,y)$ 到直线 $l$ 的“折线距离”等于 $||MF_2||$，则点 $N(t,1)$ 到点 $M$ 的轨迹的“折线距离”为  ．
【难度】
【出处】
无
【标注】
  • 方法
    >
    思考方式
    >
    信息迁移
  • 题型
    >
    解析几何
    >
    解析几何创新题
【答案】
$(1)$ $9$；$(2)$ $2$；$(3)$ $4+4\sqrt 2$；$(4)$ $\dfrac 12$；$(5)$ $ \begin{cases}-t+\dfrac 12,t \leqslant \dfrac 12,\\ t-\dfrac 12,\dfrac 12<t\leqslant \dfrac 32,\\ 1,t>\dfrac 32.\end{cases} $
【解析】
$(1)$ $||AF_1||=6$，如图1，点 $M $ 的轨迹（“折线段”）的面积为 $9$；
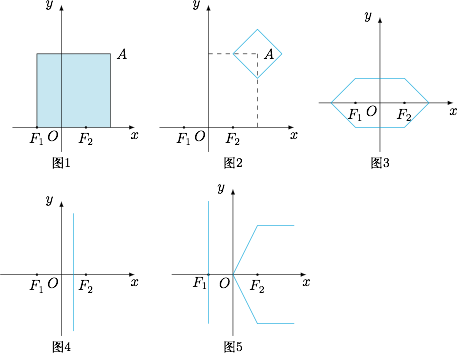
$(2)$ 如图2，点 $M$ 的轨迹（“折线圆”）所围成的面积为 $2$；
$(3)$ 如图3，点 $M$ 的轨迹（“折线椭圆”）的周长为 $4+4\sqrt 2$；
$(4)$ 如图4，原点 $O$ 到点 $M$ 的轨迹（“折线双曲线”）的“折线距离”为 $\dfrac 12$；
$(5)$ 如图5，点 $N(t,1)$ 到点 $M$ 的轨迹（“折线抛物线”）的“折线距离”为$$\begin{cases}-t+\dfrac 12,t \leqslant \dfrac 12,\\ t-\dfrac 12,\dfrac 12<t\leqslant \dfrac 32,\\ 1,t>\dfrac 32.\end{cases}$$
题目 答案 解析 备注
0.232338s