已知函数 $f(x)=\dfrac{\sin x+m}{\cos x+2}+n\cdot \tan x$ 的最大值与最小值之和为 $8$,则 $m+n$ 的值是 .
【难度】
【出处】
无
【标注】
【答案】
$6$
【解析】
因为 $\cos x+2\in [1,3]$,由函数 $f(x)$ 的有界性可得 $n=0$,接下来考虑\[y=\dfrac{\sin x+m}{\cos x+2},\]即\[\sin x-y\cos x=2y-m,\]因此\[-1\leqslant \dfrac{2y-m}{\sqrt{1+y^2}}\leqslant 1,\]也即\[3y^2-4my+m^2-1\leqslant 0.\]根据题意,关于 $y$ 的方程\[3y^2-4my+m^2-1=0\]的两根之和为 $8$,因此 $m=6$.经检验,函数\[f(x)=\dfrac{\sin x+6}{\cos x+2},x\ne \dfrac{\pi}2+k\pi,k\in\mathbb Z\]的最大值和最小值之和为 $8$,因此 $m+n$ 的值为 $6$.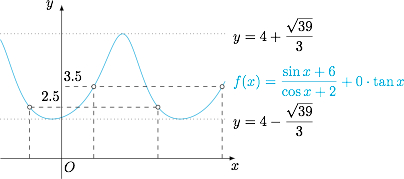

题目
答案
解析
备注