已知坐标平面 $xOy$ 上 $N$ 为圆 $x^2+y^2=1$ 上的一个动点，平面内动点 $M(x_0,y_0)$ 满足 $|y_0|\geqslant 1$ 且 $\angle OMN=30^\circ$，则动点 $M$ 运动的区域面积是 ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{8\pi}3-2\sqrt 3$
【解析】
先不考虑 $|y_0|\geqslant 1$ 的限制，考虑满足条件 $\angle OMN=30^\circ$ 的点 $M$：
选定 $N$ 后，点 $M$ 点在一个半径为 $\dfrac 12\cdot\dfrac{1}{\sin 30^\circ}=1$ 的圆的优弧上，且劣弧始终在单位圆内，$ON$ 该是圆的一条弦．如图：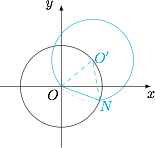
容易得到点 $M$ 所在的圆的圆心在单位圆上，于是直接考虑一个半径为 $1$ 的动圆，其圆心在单位圆 $x^2+y^2=1$ 上运动形成的轨迹，是一个以 $O$ 为圆心，$2$ 的半径的圆．于是得到 $M$ 点运动的区域为如图的阴影部分．
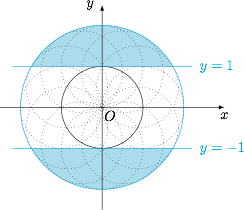根据弓形面积公式，所求面积为\[2\cdot \dfrac 12\left(\dfrac{2\pi}3-\sin\dfrac{2\pi}3\right)\cdot 2^2=\dfrac{8\pi}3-2\sqrt 3.\]
选定 $N$ 后，点 $M$ 点在一个半径为 $\dfrac 12\cdot\dfrac{1}{\sin 30^\circ}=1$ 的圆的优弧上，且劣弧始终在单位圆内，$ON$ 该是圆的一条弦．如图：
容易得到点 $M$ 所在的圆的圆心在单位圆上，于是直接考虑一个半径为 $1$ 的动圆，其圆心在单位圆 $x^2+y^2=1$ 上运动形成的轨迹，是一个以 $O$ 为圆心，$2$ 的半径的圆．于是得到 $M$ 点运动的区域为如图的阴影部分．根据弓形面积公式，所求面积为\[2\cdot \dfrac 12\left(\dfrac{2\pi}3-\sin\dfrac{2\pi}3\right)\cdot 2^2=\dfrac{8\pi}3-2\sqrt 3.\]
题目
答案
解析
备注
