已知向量 $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ 是三个具有公共起点的非零向量，且 $\left|\overrightarrow{a}\right|=2\left|\overrightarrow{b}\right|=2$，又 $\overrightarrow{a}\cdot\overrightarrow{b}=-1$，$\left\langle\overrightarrow{a}-\overrightarrow{c},\overrightarrow{b}-\overrightarrow{c}\right\rangle=\dfrac{\pi}{3}$，则当 $\left|\overrightarrow{a}-\overrightarrow{c}\right|=\sqrt7$ 时，向量 $\overrightarrow{a}$ 与 $\overrightarrow{c}$ 的夹角是 ．
【难度】
【出处】
2012年第二十三届“希望杯”全国数学邀请赛高二（二试）
【标注】
【答案】
$\dfrac{\pi}{3}$ 或 $\dfrac{\pi}{2}$
【解析】
取 $\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}$，点 $C$ 在圆弧 $\overparen{ACB}$ 上，如图．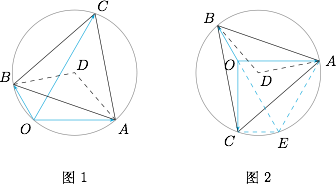
由题可知$$OA=2,OB=1,\angle ADB=\dfrac{2\pi}{3},\angle BCA=\dfrac{\pi}{3},$$结合 $\overrightarrow{OA}\cdot\overrightarrow{OB}=-1$，可解得$$AB=\sqrt7,\angle AOB=\dfrac{2\pi}{3},$$情形一 如图1，因为$$\angle ACB+\angle AOB=\pi,$$因此 $A,C,B,O$ 四点共圆，故向量 $\overrightarrow{a}$ 与 $\overrightarrow{c}$ 的夹角是 $\dfrac{\pi}{3}$；
情形二 如图2，绕点 $A$，将 $\triangle AOB$ 顺时针旋转 $\dfrac{\pi}{3}$，得到 $\triangle AEC$，连接 $OE$，故 $\triangle AOE$ 为等边三角形，$$\angle AEC=\dfrac{2\pi}{3},AE=OA=2,CE=BO=1,$$因此在 $\triangle OCE$ 中，$$OE=2,CE=1,\angle OEC=\dfrac{\pi}{3},$$可解得$$ \angle OCE=\dfrac{\pi}{2},$$在四边形 $AOCE$ 中，可得$$\angle AOC=2\pi-\angle OAE-\angle AEC-\angle ECO=\dfrac{\pi}{2},$$故向量 $\overrightarrow{a}$ 与 $\overrightarrow{c}$ 的夹角是 $\dfrac{\pi}{2}$；
综上可得，向量 $\overrightarrow{a}$ 与 $\overrightarrow{c}$ 的夹角是 $\dfrac{\pi}{3}$ 或 $\dfrac{\pi}{2}$．
由题可知$$OA=2,OB=1,\angle ADB=\dfrac{2\pi}{3},\angle BCA=\dfrac{\pi}{3},$$结合 $\overrightarrow{OA}\cdot\overrightarrow{OB}=-1$，可解得$$AB=\sqrt7,\angle AOB=\dfrac{2\pi}{3},$$综上可得，向量 $\overrightarrow{a}$ 与 $\overrightarrow{c}$ 的夹角是 $\dfrac{\pi}{3}$ 或 $\dfrac{\pi}{2}$．
题目
答案
解析
备注
