已知正方体 $ABCD-A_1B_1C_1D_1$ 的棱长为 $1$，$O$ 为底面 $ABCD$ 的中心，$M,N$ 分别是棱 $A_1D_1$ 和 $CC_1$ 的中点，则四面体 $O-MNB_1$ 的体积为 ．
【难度】
【出处】
2009年全国高中数学联赛湖北省预赛
【标注】
【答案】
$\dfrac{7}{48}$
【解析】
如图，倍长 $MO$ 至 $P$，连接 $PB_1,PN$．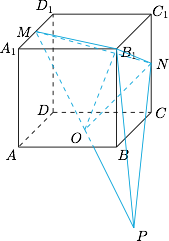
根据题意，有\[O-MNB_1=\dfrac 12P-MNB_1=\dfrac 12M-PNB_1=\dfrac 12\cdot \dfrac 13\cdot 1\cdot \dfrac 78=\dfrac{7}{48}.\]
根据题意，有\[O-MNB_1=\dfrac 12P-MNB_1=\dfrac 12M-PNB_1=\dfrac 12\cdot \dfrac 13\cdot 1\cdot \dfrac 78=\dfrac{7}{48}.\]
题目
答案
解析
备注
