将一个四棱锥的每个顶点染上一种颜色,并使每条棱的两端点异色,若只有 $5$ 种颜色可供使用,则不同的染色方法的总数为 \((\qquad)\)
【难度】
【出处】
2007年复旦大学优秀高中生文化水平选拔测试
【标注】
【答案】
D
【解析】
如图.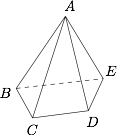
情形一 用 $5$ 种颜色,方法数为\[{\mathrm {A}}_5^5.\]情形二 用 $4$ 种颜色,只可能 $B,D$ 同色或 $C,E$ 同色,方法数为\[{\mathrm {C}}_5^4{\mathrm {A}}_4^3 \cdot 2.\]情形三 用 $3$ 种颜色,则 $B,D$ 同色,且 $C,E$ 同色,方法数为\[{\mathrm {C}}_5^3 \cdot {\mathrm {A}}_3^3.\]所以不同的染色方法的总数为\[120 + 240 + 60 = 420.\]

题目
答案
解析
备注