设 $\overrightarrow {AB}=(2,3)$，$\overrightarrow {AC}=(1,k)$，在 $\triangle ABC$ 中，若 $\angle A=90^{\circ}$，则 $k=$ ；若 $\angle B=90^{\circ}$，则 $k=$ ；若 $\angle C=90^{\circ}$，则 $k=$ ．
【难度】
【出处】
2009年第二十届“希望杯”全国数学邀请赛高一（一试）
【标注】
【答案】
$-\dfrac 23$；$\dfrac {11}{3}$；$\dfrac {3\pm \sqrt{13}}{2}$
【解析】
如图．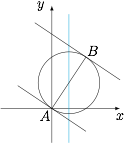
所求分别为\[\begin{split} l_1&:y=-\dfrac 23x,\\
l_2&:y=-\dfrac 23(x-2)+3,\\
l_3&:x(x-2)+y(y-3)=0,\end{split}\]与直线 $x=1$ 的交点纵坐标．
所求分别为\[\begin{split} l_1&:y=-\dfrac 23x,\\l_2&:y=-\dfrac 23(x-2)+3,\\
l_3&:x(x-2)+y(y-3)=0,\end{split}\]与直线 $x=1$ 的交点纵坐标．
题目
答案
解析
备注
