查看数据源：5a041821e1d4630009e6d4ae
对于三个侧面两两垂直的三棱锥，给出如下四个命题：
① 该棱锥的底面是锐角三角形；
② 该棱锥的顶点在底面内的射影是底面三角形的垂心；
③ 该棱锥的三组对棱都互相垂直；
④ 该棱锥的底面是正三角形．
其中正确命题的序号是 ．
【难度】
【出处】
2009年第二十届“希望杯”全国数学邀请赛高一（一试）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间组合体
    >
    空间几何体的补形
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
【答案】
①②③
【解析】
如图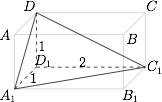．对于命题 ①，因为底面三角形的任意两边的平方和都大于第三边的平方，所以根据余弦定理知，底面三角形的每个角都是锐角，故该棱锥的底面是锐角三角形（也可以根据三余弦定理进行判断）．
对于命题 ②，因为三棱锥的三个侧面两两垂直，所以三棱锥的对棱互相垂直；
对于命题 ③，对棱中一棱在底面射影与另一棱垂直，故棱锥的顶点在底面内的射影是底面三角形的垂心；
对于命题 ④，图中棱锥 $A_1C_1D-D_1$ 底面 $\triangle A_1C_1D$ 不为等边三角形．
所以正确命题的序号是 ①②③．
题目 答案 解析 备注
0.203891s