正方体 $ABCD-A_1B_1C_1D_1$ 的棱长为 $1$，$E$，$F$，$G$，$H$ 分别是正方形 $A_1B_1C_1D_1$ 四边的中点．在 $A,B,C,D,E,F,G,H$ 这 $8$ 个点中任取 $3$ 个点组成三角形，这些三角形按不同的面积分类，共有 类，其中最大的面积等于 ．
【难度】
【出处】
2009年第二十届“希望杯”全国数学邀请赛高一（一试）
【标注】
【答案】
$7$；$\dfrac {\sqrt2}{2}$
【解析】
分情况讨论，如图．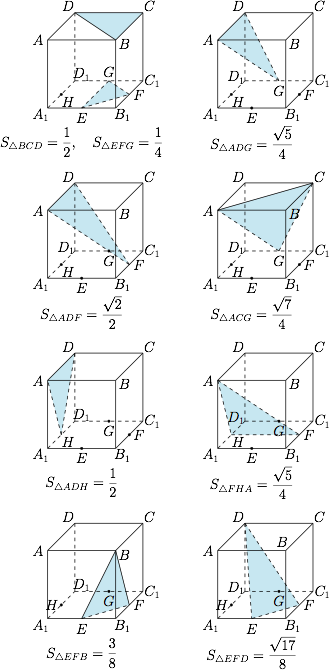
可知，三角形的不同面积有\[\dfrac {1}{4},\dfrac {3}{8},\dfrac {1}{2},\dfrac {\sqrt {17}}{8},\dfrac {\sqrt 5}{4},\dfrac {\sqrt 7}{4},\dfrac {\sqrt2}{2},\]共 $7$ 类，其中最大的面积等于 $\dfrac {\sqrt 2}{2}$．
可知，三角形的不同面积有\[\dfrac {1}{4},\dfrac {3}{8},\dfrac {1}{2},\dfrac {\sqrt {17}}{8},\dfrac {\sqrt 5}{4},\dfrac {\sqrt 7}{4},\dfrac {\sqrt2}{2},\]共 $7$ 类，其中最大的面积等于 $\dfrac {\sqrt 2}{2}$．
题目
答案
解析
备注
