在正四面体 $V-ABC$ 中，点 $E,F,G,H$ 分别是边 $AB,AC,VB,VC$ 的中点．则平面 $AGH$ 与平面 $VEF$ 的夹角大小为 ．
【难度】
【出处】
2009年第二十届“希望杯”全国数学邀请赛高二（二试）
【标注】
【答案】
$\arccos \dfrac7{11}$
【解析】
记正四面体棱长为 $1$，如图所示，$M,N$ 分别是线段 $GH$ 与 $EF$ 的中点，$O$ 为 $AM$ 与 $VN$ 的交点．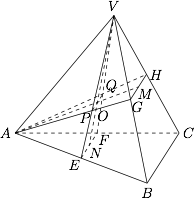
根据题意，有有$$\begin{split} &VP=\dfrac23VE=\dfrac23\cdot\dfrac{\sqrt3}2=\dfrac{\sqrt3}3,\\
&OP=\dfrac23EN=\dfrac16BC=\dfrac16,\end{split}$$故$$VO=\sqrt{VP^2-OP^2}=\sqrt{\dfrac13-\dfrac1{36}}=\dfrac{\sqrt{11}}6,$$又 $AO=VO$，于是由余弦定理$$\cos \angle AOV=\dfrac{VO^2+AO^2-AV^2}{2VO\cdot AO}=-\dfrac7{11},$$故所求两平面夹角大小为 $\arccos\dfrac7{11}$．
根据题意，有有$$\begin{split} &VP=\dfrac23VE=\dfrac23\cdot\dfrac{\sqrt3}2=\dfrac{\sqrt3}3,\\&OP=\dfrac23EN=\dfrac16BC=\dfrac16,\end{split}$$故$$VO=\sqrt{VP^2-OP^2}=\sqrt{\dfrac13-\dfrac1{36}}=\dfrac{\sqrt{11}}6,$$又 $AO=VO$，于是由余弦定理$$\cos \angle AOV=\dfrac{VO^2+AO^2-AV^2}{2VO\cdot AO}=-\dfrac7{11},$$故所求两平面夹角大小为 $\arccos\dfrac7{11}$．
题目
答案
解析
备注
