已知点 $E,F$ 分别在正方体 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 的棱 $B{B_1},C{C_1}$ 上，且 ${B_1}E = 2EB$，$CF = 2F{C_1}$，则面 $AEF$ 与面 $ABC$ 所成的二面角的正切值等于 ．
【难度】
【出处】
2011年高考大纲全国卷（理）
【标注】
【答案】
$\dfrac{\sqrt 2 }{3}$
【解析】
如图，延长 $FE$ 交 $CB$ 的延长线于 $G$，连接 $AG$，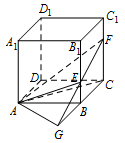
则 $AG$ 为面 $AEF$ 与面 $ABC$ 的交线．
由\[{B_1}E = 2EB,CF = 2F{C_1},\]得\[CF = 2BE,\]$\therefore$ $B$ 为 $GC$ 中点．设正方体的棱长为 $ 1 $，则\[AG = AC = \sqrt 2 ,\]又 $GC = 2$，所以\[A{C^2} + A{G^2} = G{C^2},\]所以\[\angle CAG = 90^\circ ,\]$\because$ $FC \perp $ 平面 $ABC$，$\therefore$ $FA \perp AG$，$\therefore$ $\angle CAF$ 是面 $AEF$ 与面 $ABC$ 所成的二面角的平面角，
在 ${\mathrm{Rt}}\triangle ACF$ 中，\[\tan \angle CAF = \dfrac{CF}{AC} = \dfrac{{\dfrac{2}{3}}}{\sqrt 2 } = \dfrac{\sqrt 2 }{3},\]故面 $AEF$ 与面 $ABC$ 所成的二面角的正切值等于 $\dfrac{\sqrt 2 }{3}$．
则 $AG$ 为面 $AEF$ 与面 $ABC$ 的交线．由\[{B_1}E = 2EB,CF = 2F{C_1},\]得\[CF = 2BE,\]$\therefore$ $B$ 为 $GC$ 中点．设正方体的棱长为 $ 1 $，则\[AG = AC = \sqrt 2 ,\]又 $GC = 2$，所以\[A{C^2} + A{G^2} = G{C^2},\]所以\[\angle CAG = 90^\circ ,\]$\because$ $FC \perp $ 平面 $ABC$，$\therefore$ $FA \perp AG$，$\therefore$ $\angle CAF$ 是面 $AEF$ 与面 $ABC$ 所成的二面角的平面角，
在 ${\mathrm{Rt}}\triangle ACF$ 中，\[\tan \angle CAF = \dfrac{CF}{AC} = \dfrac{{\dfrac{2}{3}}}{\sqrt 2 } = \dfrac{\sqrt 2 }{3},\]故面 $AEF$ 与面 $ABC$ 所成的二面角的正切值等于 $\dfrac{\sqrt 2 }{3}$．
题目
答案
解析
备注
