在正三角形 $ABC$ 中，$D$ 是 $BC$ 上的点．若 $AB = 3$，$BD = 1$，则 $\overrightarrow {AB} \cdot \overrightarrow {AD} = $ ．
【难度】
【出处】
2011年高考上海卷（理）
【标注】
【答案】
$\dfrac {15} 2 $
【解析】
如图：过点 $D$ 作 $DE \perp AB$ 于 $E $．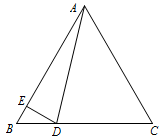
则\[\overrightarrow {AB} \cdot \overrightarrow {AD} = \overrightarrow {AB} \cdot \overrightarrow {AE} = 3\left| {\overrightarrow {AE} } \right| = 3\left( {3 - \dfrac{1}{2}BD} \right) = \dfrac{15}{2}.\]
则\[\overrightarrow {AB} \cdot \overrightarrow {AD} = \overrightarrow {AB} \cdot \overrightarrow {AE} = 3\left| {\overrightarrow {AE} } \right| = 3\left( {3 - \dfrac{1}{2}BD} \right) = \dfrac{15}{2}.\]
题目
答案
解析
备注
