如图,在梯形 $ABCD$ 中,$AB\parallel CD$,$AB=4 $,$CD=2 $,$E、F$ 分别为 $AD、BC$ 上的点,且 $EF=3 $,$EF\parallel AB$,则梯形 $ABFE$ 与梯形 $EFCD $ 的面积比为 .

【难度】
【出处】
2011年高考广东卷(文)
【标注】
【答案】
$\dfrac{7}{5}$
【解析】
如图,分别延长 $AD、BC$,且 $AD \cap BC =P $.
因为 $\dfrac{CD}{EF} = \dfrac{2}{3},$ 所以 $\dfrac{{{S_{\triangle PCD}}}}{{{S_{\triangle PEF}}}} = \dfrac{4}{9}$;
因为 $\dfrac{CD}{AB} = \dfrac{2}{4},$ 所以 $\dfrac{{{S_{\triangle PCD}}}}{{{S_{\triangle PAB}}}} = \dfrac{4}{16}$,所以 $\dfrac{{{S_{梯形ABEF}}}}{{{S_{梯形EFCD}}}} = \dfrac{7}{5}$.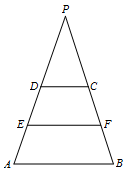
因为 $\dfrac{CD}{EF} = \dfrac{2}{3},$ 所以 $\dfrac{{{S_{\triangle PCD}}}}{{{S_{\triangle PEF}}}} = \dfrac{4}{9}$;
因为 $\dfrac{CD}{AB} = \dfrac{2}{4},$ 所以 $\dfrac{{{S_{\triangle PCD}}}}{{{S_{\triangle PAB}}}} = \dfrac{4}{16}$,所以 $\dfrac{{{S_{梯形ABEF}}}}{{{S_{梯形EFCD}}}} = \dfrac{7}{5}$.

题目
答案
解析
备注