查看数据源：5a03cd5fe1d4630009e6d31a
已知函数 $ f\left(x\right)=\log_2{\left(x+2\right)} $ 与 $ g\left(x\right)=\left(x-a\right)^{2}+1 $，若对任意的 $ x_{1}\in\left[2,6\right) $，都存在 $ x_{2}\in\left[0,2\right]$，使得 $ f\left(x_{1}\right)=g\left(x_{2}\right) $，则实数 $ a $ 的取值范围是  ．
【难度】
【出处】
无
【标注】
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    二次函数
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    对数函数
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的最值和值域
【答案】
$ \left[-1,2-\sqrt{2}\right]\cup\left[\sqrt{2},3\right] $
【解析】
根据题意，有\[\left\{{\log_2}(x+2)\mid x\in [2,6)\right\}\subseteq \left\{(x-a)^2+1 \mid x\in [0,2]\right\},\]也即\[[2,3]\subseteq \left\{(x-a)^2+1\mid x\in [0,2]\right\},\]也即\[[1,2]\subseteq \left\{x^2\mid x\in [-a,2-a]\right\}.\]如图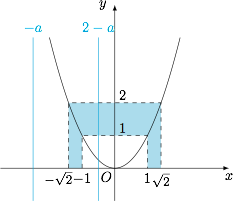．可解得实数 $a$ 的取值范围是 $ \left[-1,2-\sqrt{2}\right]\cup\left[\sqrt{2},3\right] $．
题目 答案 解析 备注
0.114569s