已知点 $P$ 是 $\triangle ABC$ 内任一点，且满足 $\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AC}$，则 $2x+y$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$(0,2)$
【解析】
取 $AB$ 中点，记为 $D$，如图．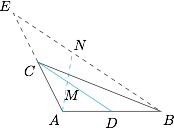
题中等式即$$\overrightarrow{AP}=2x\cdot\overrightarrow{AD}+y\cdot\overrightarrow{AC},$$设直线 $AP$ 与线段 $CD$ 交于点 $M$，$BE$ 于点 $N$，则有$$\overrightarrow{AP}=\lambda\overrightarrow{AM}=\lambda\left(m\cdot\overrightarrow{AD}+n\cdot\overrightarrow{AC}\right),$$结合 $C,D,M$ 三点共线，可知 $m+n=1$，进而$$2x+y=\lambda=\dfrac{AP}{AM}<\dfrac{AN}{AM}\leqslant2,$$结合点 $P$ 在 $\triangle ABC$ 内，可得 $x,y>0$，进而 $2x+y$ 的取值范围是 $(0,2)$．
题中等式即$$\overrightarrow{AP}=2x\cdot\overrightarrow{AD}+y\cdot\overrightarrow{AC},$$设直线 $AP$ 与线段 $CD$ 交于点 $M$，$BE$ 于点 $N$，则有$$\overrightarrow{AP}=\lambda\overrightarrow{AM}=\lambda\left(m\cdot\overrightarrow{AD}+n\cdot\overrightarrow{AC}\right),$$结合 $C,D,M$ 三点共线，可知 $m+n=1$，进而$$2x+y=\lambda=\dfrac{AP}{AM}<\dfrac{AN}{AM}\leqslant2,$$结合点 $P$ 在 $\triangle ABC$ 内，可得 $x,y>0$，进而 $2x+y$ 的取值范围是 $(0,2)$．
题目
答案
解析
备注
