$ABCD-A_1B_1C_1D_1$ 是正方体，则二面角 $A-DB_1-B$ 的大小等于 ．
【难度】
【出处】
2009年第二十届“希望杯”全国数学邀请赛高一（二试）
【标注】
【答案】
$60^{\circ}$
【解析】
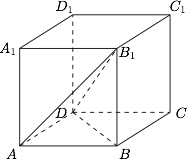设所求二面角的大小为 $\varphi$，则根据三射线定理，有\[\cos\angle ADB=\cos\angle ADB_1\cdot\cos\angle BDB_1+\sin\angle ADB_1\cdot \sin\angle BDB_1\cdot \cos\varphi,\]于是\[\dfrac{\sqrt 2}2=\dfrac{1}{\sqrt 3}\cdot \dfrac{\sqrt 2}{\sqrt 3}+\dfrac{\sqrt 2}{\sqrt 3}\cdot \dfrac{1}{\sqrt 3}\cdot \cos\varphi,\]解得 $\cos\varphi=\dfrac 12$，于是 $\varphi=60^\circ$．
题目
答案
解析
备注
