当 $a=0$ 时显然符合题意．
当 $a\ne 0$ 时，函数\[f(x)=\begin{cases}x^2+ax+1,&ax+1<0,\\ x^2-ax-1,&ax+1\geqslant 0,\end{cases}\]因此 $f(x)$ 的图象是两条抛物线以 $x=-\dfrac 1a$ 为界“接驳”而成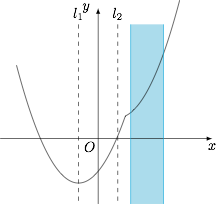．考虑到它们的对称轴分别为 $x=-\dfrac a2$ 和 $x=\dfrac a2$．
情形一当 $a>0$ 时，有 $-\dfrac 1a<0$，函数 $f(x)$ 在 $[1,2]$ 上的递增性由右侧的抛物线 $y=x^2-ax-1$ 提供，此时有 $\dfrac a2\leqslant 1$，于是 $0<a\leqslant 2$．
情形二 当 $a<0$ 且 $0<-\dfrac 1a\leqslant 1$，即 $a\leqslant -1$ 时，函数 $f(x)$ 在 $[1,2]$ 上的递增性由右侧的抛物线 $y=x^2+ax+1$ 提供，此时有 $-\dfrac a2\leqslant 1$，于是 $-2\leqslant a\leqslant -1$．
情形三当 $-\dfrac 1a>1$，即 $-1<a<0$ 时，左边的抛物线 $y=x^2-ax-1$ 在 $\left(\dfrac a2,-\dfrac 1a\right)$ 上单调递增．又 $ -\dfrac a2<\dfrac 12 $，所以右侧的抛物线 $y=x^2+ax-1$ 在 $\left(-\dfrac 1a,+\infty\right)$ 上单调递增，所以此时符合题意．
综上所述，所求的实数 $ a $ 的取值范围是 $ [-2,2]$．