已知直线 $l_1:x+2y-4=0$,直线 $l_2:2ax-y+1=0$ 和坐标轴围成的四边形有外接圆,则 $a$ 的值等于 .
【难度】
【出处】
2009年第二十届“希望杯”全国数学邀请赛高二(一试)
【标注】
【答案】
$\pm1$
【解析】
题意即两直线与坐标轴围成的四边形的对角和为 $\pi$,设直线 $l_1,l_2$ 的倾斜角分别为 $\theta_1,\theta_2$,直线 $l_2$ 经过定点 $(0,1)$.
情形一 满足题意的直线如图1时,此时$$\theta_1+\theta_2=\dfrac{\pi}{2},$$解得 $a=1$;
情形二 满足题意的直线如图2时,此时$$\theta_2=\theta_1+\dfrac{\pi}{2},$$解得 $a=-1$;
综上可知 $a$ 的值等于 $\pm1$.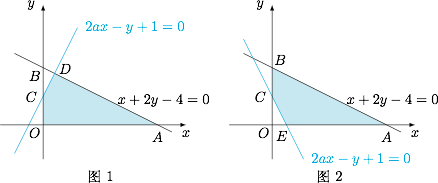
综上可知 $a$ 的值等于 $\pm1$.

题目
答案
解析
备注