棱长为 $1$ 的正方体 $ABCD-A_1B_1C_1D_1$ 中，$E,F,E_1,F_1$ 分别是边 $AD,AB,B_1C_1,C_1D_1$ 的中点，作过 $EF,E_1F_1$ 的平面 $\alpha$，则 $\alpha$ 和平面 $ABCD$ 所成的二面角的大小是 ，立方体 $ABCD-A_1B_1C_1D_1$ 被 $\alpha$ 截得的截面的面积等于 ．
【难度】
【出处】
2009年第二十届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$\arccos\dfrac{\sqrt3}{3}$；$\dfrac{3\sqrt3}{4}$
【解析】
取 $BC$ 中点，记为 $H$，连接 $E_1H,FH$，如图．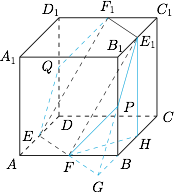
则 $\angle E_1FH$ 即为 $\alpha$ 与平面 $ABCD$ 所成的二面角，在 $\triangle E_1FH$ 中，$$\cos\angle E_1FH=\dfrac{FH}{E_1F}=\dfrac{\sqrt3}{3},$$因此 $\alpha$ 和平面 $ABCD$ 所成的二面角的大小是 $\arccos\dfrac{\sqrt3}{3}$．
在平面 $ABCD$ 中，延长 $EF$ 交 $CB$ 于点 $G$，连接 $E_1G$ 交 $BB_1$ 于点 $P$，由正方体 $ABCD-A_1B_1C_1D_1$，可知点 $P$ 为 $BB_1$ 的中点，根据对称性可知 $\alpha$ 截正方体的截面为正六面体 $EFPE_1F_1Q$，其中 $Q$ 为 $DD_1$ 的中点，因此截面的面积为$$6\cdot\dfrac{\sqrt3}{4}\cdot EF^2=\dfrac{3\sqrt3}{4}.$$
则 $\angle E_1FH$ 即为 $\alpha$ 与平面 $ABCD$ 所成的二面角，在 $\triangle E_1FH$ 中，$$\cos\angle E_1FH=\dfrac{FH}{E_1F}=\dfrac{\sqrt3}{3},$$因此 $\alpha$ 和平面 $ABCD$ 所成的二面角的大小是 $\arccos\dfrac{\sqrt3}{3}$．在平面 $ABCD$ 中，延长 $EF$ 交 $CB$ 于点 $G$，连接 $E_1G$ 交 $BB_1$ 于点 $P$，由正方体 $ABCD-A_1B_1C_1D_1$，可知点 $P$ 为 $BB_1$ 的中点，根据对称性可知 $\alpha$ 截正方体的截面为正六面体 $EFPE_1F_1Q$，其中 $Q$ 为 $DD_1$ 的中点，因此截面的面积为$$6\cdot\dfrac{\sqrt3}{4}\cdot EF^2=\dfrac{3\sqrt3}{4}.$$
题目
答案
解析
备注
