设 $A\left(0,0\right)$,$B\left(4,0\right)$,$C\left(t + 4,3\right)$,$D\left(t,3\right) \left(t \in {\mathbb{R}}\right)$.记 $N\left(t\right)$ 为平行四边形 $ABCD$ 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则 $N\left(0\right) = $ ;$N\left(t\right)$ 的所有可能取值为 .
【难度】
【出处】
2011年高考北京卷(文)
【标注】
【答案】
$6$;$6,7,8$
【解析】
当 $t = 0$ 时,作图易知共有 $6$ 个整点,即 $N\left( 0 \right) = 6$;如图分别确定直线 $AD$,$BC$ 的方程,然后确定直线 $y = 1$,$y = 2$ 与其交点的坐标依次为\[E\left( {\dfrac{t}{3},1} \right),G\left( {\dfrac{t}{3} + 4,1} \right) , F\left( {\dfrac{2t}{3},2} \right) ,H\left( {\dfrac{2t}{3} + 4,2} \right),\]故当 $\dfrac{t}{3} \in {\mathbb{Z}}$ 时,则 $\dfrac{2t}{3} \in {\mathbb{Z}}$,在线段 $GE$ 上且在平行四边形内部的整点共有 $3$ 个,在线段 $FH$ 上且在平行四边形内部的整点共有 $3$ 个,此时整点的个数共有 $6$ 个;
当 $\dfrac{t}{3} \notin {\mathbb{Z}}$,$\dfrac{2t}{3} \in {\mathbb{Z}}$ 时,线段 $GE$ 上满足条件的整点有 $4$ 个,$FH$ 上共有 $3$ 个,故整点总数为 $7$ 个;
当 $\dfrac{t}{3} \notin {\mathbb{Z}}$,$\dfrac{2t}{3} \notin {\mathbb{Z}}$ 时,线段 $EG$,$FH$ 上各有 $4$ 个整点在平行四边形内部,故此时整点个数共有 $8$ 个,综上可知 $N\left(t\right)$ 的所有取值为 $6$,$7$,$8$.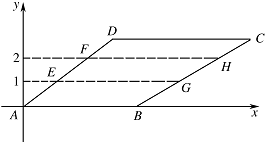
当 $\dfrac{t}{3} \notin {\mathbb{Z}}$,$\dfrac{2t}{3} \in {\mathbb{Z}}$ 时,线段 $GE$ 上满足条件的整点有 $4$ 个,$FH$ 上共有 $3$ 个,故整点总数为 $7$ 个;
当 $\dfrac{t}{3} \notin {\mathbb{Z}}$,$\dfrac{2t}{3} \notin {\mathbb{Z}}$ 时,线段 $EG$,$FH$ 上各有 $4$ 个整点在平行四边形内部,故此时整点个数共有 $8$ 个,综上可知 $N\left(t\right)$ 的所有取值为 $6$,$7$,$8$.

题目
答案
解析
备注