如图所示，用边长 $40\mathrm{cm}$ 的正方形铁皮 $ABCD$ 做簸箕，做法：取 $AB$ 边中点 $E$，连结 $CE$，$DE$，沿 $CE$ 和 $DE$ 将 $\triangle ADE$ 和 $\triangle BCE$ 折起来并将边 $EA$ 和 $EB$ 焊接起来，此时 $A$ 与 $B$ 重合于点 $O$，那么这个簸箕状几何体的容积是 $\mathrm{cm}^3$．
【难度】
【出处】
2008年第十九届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$\dfrac{8000\sqrt 3}3$
【解析】
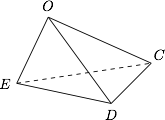根据题意易知 $OE\perp OCD$，且$$OC=OD=CD=40,$$所以簸箕状几何体的容积为\[\dfrac 13\cdot \triangle OCD\cdot EO=\dfrac{8000\sqrt 3}3.\]
题目
答案
解析
备注
