如图，正方形 $ABCD$ 和 $ABEF$ 的边长都是 $a$，平面 $ABCD\perp$ 平面 $ABEF$，点 $M,N$ 分别在 $AC$，$BF$ 上移动，且 $CM=BN$．记 $CM$ 与 $BN$ 的长为 $x$，$MN$ 的长为 $f(x)$，则 $f(x)=$ ，其最小值为 ．
【难度】
【出处】
2008年第十九届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$f(x)=\sqrt{x^2-\sqrt2ax+a^2},0\leqslant x\leqslant 2a$，$f(x)$ 的最小值为 $\dfrac{\sqrt2}{2}a$
【解析】
如图，过 $M$ 作 $MP\parallel AB$ 交 $BC$ 于 $P$，连接 $NP$，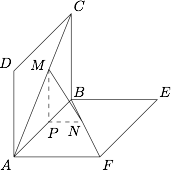
易知 $NP\parallel AF$，且 $AB\perp$ 面 $PMN$，则$$\begin{split} f(x)&=MN=\sqrt{MP^2+NP^2}\\
&=\sqrt{\left(a-\dfrac{\sqrt2}{2}x\right)^2+\left(\dfrac{\sqrt2}{2}x\right)^2}\\
&=\sqrt{x^2-\sqrt2ax+a^2},\end{split}$$其中$$0\leqslant x\leqslant 2a.$$所以$$f(x)=\sqrt{\left(x-\dfrac{\sqrt2}{2}a\right)^2+\dfrac12a^2}\geqslant\dfrac{\sqrt2}{2}a,$$当 $x=\dfrac{\sqrt2}{2}a$ 时，上述不等式取得等号，因此 $f(x)$ 的最小值为 $\dfrac{\sqrt2}{2}a$．
易知 $NP\parallel AF$，且 $AB\perp$ 面 $PMN$，则$$\begin{split} f(x)&=MN=\sqrt{MP^2+NP^2}\\&=\sqrt{\left(a-\dfrac{\sqrt2}{2}x\right)^2+\left(\dfrac{\sqrt2}{2}x\right)^2}\\
&=\sqrt{x^2-\sqrt2ax+a^2},\end{split}$$其中$$0\leqslant x\leqslant 2a.$$所以$$f(x)=\sqrt{\left(x-\dfrac{\sqrt2}{2}a\right)^2+\dfrac12a^2}\geqslant\dfrac{\sqrt2}{2}a,$$当 $x=\dfrac{\sqrt2}{2}a$ 时，上述不等式取得等号，因此 $f(x)$ 的最小值为 $\dfrac{\sqrt2}{2}a$．
题目
答案
解析
备注
