在 $\triangle ABC$ 中，点 $D,E$ 分别在边 $BC$ 和 $AC$ 上，且 $BD=\dfrac25 BC$，$CE=\dfrac13 CA$，$AD,BE$ 交于点 $R$，，则 $\dfrac{RD}{AD}=$ ，$\dfrac{RE}{BE}=$ ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac16,\dfrac12$
【解析】
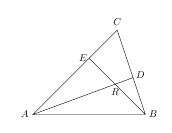根据梅涅劳斯定理，因为 $\triangle BCE$ 被直线 $ARD$ 所截，所以$$\dfrac{CA}{AE}\cdot\dfrac{ER}{RB}\cdot\dfrac{BD}{DC}=1,$$又因$$\dfrac{CA}{AE}=\dfrac32,\dfrac{BD}{CD}=\dfrac23,$$所以$$\dfrac{ER}{RB}=1,\dfrac{RE}{BE}=\dfrac12,$$同理，因为 $\triangle ACD$ 被直线 $BRE$ 所截，所以$$\dfrac{AR}{RD}\cdot\dfrac{DB}{BC}\cdot\dfrac{CE}{EA}=1,$$于是$$\dfrac{AR}{RD}=5,\dfrac{RD}{AD}=\dfrac16.$$
题目
答案
解析
备注
