在 $\triangle ABC$ 中，点 $D,E$ 分别在边 $BC$ 和 $AC$ 上，且 $BD=\dfrac25 BC$，$CE=\dfrac13 CA$，$AD,BE$ 交于点 $R$，，则 $\dfrac{RD}{AD}=$ ，$\dfrac{RE}{BE}=$ ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac16,\dfrac12$
【解析】
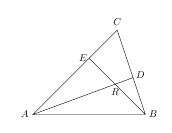根据题意设$$\begin{split} \overrightarrow{RD}=\lambda \overrightarrow{AD}, \overrightarrow{RE}=\mu\overrightarrow{BE}, \end{split}$$则有$$\overrightarrow RD=\lambda(\overrightarrow AD+\overrightarrow{CD})=\lambda\overrightarrow{AC}+\dfrac{3\lambda}{5}\overrightarrow{CB},$$又因为$$\begin{split} \overrightarrow{RD}&=\overrightarrow{RB}+\overrightarrow{BD}\\&=-\overrightarrow{BR}-\overrightarrow{DB}\\
&=-(1-\mu)\overrightarrow{BE}+\dfrac25\overrightarrow{BC}\\
&=-(1-\mu)(\overrightarrow{BC}+\overrightarrow{CE})+\dfrac25\overrightarrow{BC}\\
&=\left[(1-\mu)-\dfrac25\right]\overrightarrow{CB}-(1-\mu)\cdot\left(-\dfrac13\right)\overrightarrow{AC}\\
&=\dfrac{1-\mu}{3}\cdot\overrightarrow{AC}+\left(\dfrac35-\mu\right)\cdot\overrightarrow{CB}.
\end{split}$$所以$$\left(\lambda,\dfrac{3\lambda}{5}\right)=\left(\dfrac{1-\mu}{3},\dfrac35-\mu\right),$$解得$$(\lambda,\mu)=\left(\dfrac16,\dfrac12\right).$$
题目
答案
解析
备注
