若正方体 $ABCD-A_1B_1C_1D_1$ 的棱长为 $a$,则棱 $B_1C_1$ 和体对角线 $BD_1$ 间的距离为 .
【难度】
【出处】
2008年第十九届“希望杯”全国数学邀请赛高一(二试)
【标注】
【答案】
$ \dfrac {\sqrt 2 }{2}$
【解析】
取 $B_1C_1$ 的中点 $E$,$BD_1$ 的中点 $F$,连接 $EF$.易得$$EF \perp B_1C_1, EF \perp BD_1,$$故 $EF=\dfrac {\sqrt 2 }{2}$ 即为所求.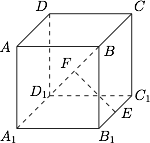

题目
答案
解析
备注